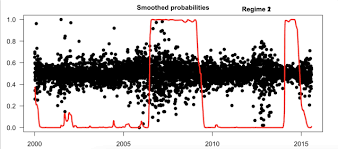
مدل‌های تغییر مارکوف

مدل‌های تغییر مارکوف (Markov-switching models) ابزار قدرتمندی برای بررسی رفتار واقعی داده‌های سری زمانی ارائه می‌دهند.

مدل‌های سری زمانی کلاسیک فرض می‌کنند که می‌توان از یک مجموعه از پارامترهای مدل برای توصیف رفتار داده‌ها در تمام زمان‌ها استفاده کرد. این فرض همیشه برای آنچه در داده های دنیای واقعی با آن مواجه می شویم معتبر نیست.

داده‌های سری زمانی در دنیای واقعی ممکن است در دوره‌های زمانی مختلف ویژگی‌های متفاوتی مانند میانگین و واریانس متفاوت داشته باشند. مدل های تغییر رژیم این امکان را فراهم می­کنند که بتوان داده‌ها را در «رژیم‌های» متفاوت و تکرارشونده قرار داد و به میانگین­ و واریانس داده­های سری زمانی و پارامترهای مدل اجازه می­دهد تا در رژیم ها تغییر کنند.

فرض کنید در هر بازه زمانی معین، این احتمال وجود دارد که سری در یکی از رژیم­­ها باشد و ممکن است به رژیم دیگر منتقل شود.

این ویژگی­ها باعث می­شوند که مدل‌های تغییر رژیم بتوانند رفتار واقعی داده‌ها را بهتر از مدل‌های استاندارد ثبت کنند.

Applications of Actuarial Model in Automobile Insurance Claim

Abstract

In this paper we apply actuarial models to detailed, micro-level automobile insurance records. As we know, third party insurance is an important major for both policyholders and insurance companies. We modeling claim frequency, type and severity of third party insurance claims with incorporate different individual and vehicle risk factors such as vehicle age, vehicle usage, vehicle capacity and no of claim discount. This allows the actuary to differentiate prices based on policyholder characteristics. In addition, by using of various risk measures, including value at risk and tail value at risk to predict the insurance company capital requirement. Finally, we assessed the effects of dependence structure on these measures by using copula models. The result shows that the copula effect is increases with the percentile.   

 

Keywords: Third party liability insurance, Risk factors, Copula, Risk measures, Capital requirement,

Mathematics Subject Classification [2020]:  91G70, 62H05 

مقدمه ای بر علم اکچوئری

با عرض سلام و ادب خدمت دوستان عزیز!

با توجه به پرسش­های متعدد دوستان در مورد آشنایی با رشته اکچوئری، بهتر دیدم که مطلبی کلی در مورد آشنایی اولیه در خصوص علم اکچوئری و رشته اکچوئری در وبلاگ قرار دهم. امیدوارم برای دوستان مفید واقع شود.

علم اکچوئری

علم اکچوئری، علمی است که با بهره­گیری از روش­های ریاضی و آماری به ارزیابی ریسک در صنایع بیمه، مالی و سایر صنایع و حرفه­های مرتبط می­پردازد. به طور کلی اکچوئری­ها از روش­های دقیق ریاضیاتی و آماری برای مدلسازی موضوعات مرتبط با عدم اطمینان جهت پیش­بینی رخدادهای آتی و محاسبه معیارهای پیشگیرانه استفاده می­کنند.

رشته اکچوئری یک رشته بین رشته­ای محسوب می­شود و تلفیقی از علوم ریاضی، آمار، مالی و بیمه است. این رشته زمینه­ های کاربردی وسیعی دارد. به طور کلی می توان زمینه های اصلی زیر را نام برد:

• صنعت بیمه (بیمه های اشخاص و بیمه های غیر اشخاص)
• صنعت بازنشستگی (مزایای بازنشستگی، مزایای درمانی، تأمین اجتماعی)
• صنعت خدمات مالی (سرمایه گذاری، مدیریت ریسک، مشاوه مالی فردی)

در بیمه­های اشخاص اغلب از روش­های ریاضیات اکچوئری در محاسبات حق بیمه و ذخایر استفاده می­شود و مفاهیم ارزش فعلی تعهدات بسیار حائز اهمیت است.

در شاخه بیمه­های غیراشخاص از روش­های آماری و احتمالی و به طور خاص نظریه ریسک استفاده می­شود. در این حوزه برازش­ توزیع­های مناسب آماری، آشنایی با روش­های نرخگذاری مانند روش­های تعمیم یافته خطی (GLM)، سیستم­های پاداش و جریمه  و ... دارای اهمیت می­باشند.

سایر حوزه­های مهم در حوزه­ی بیمه تعیین ذخایر، توانگری مالی و مدیریت ریسک شرکت­ های بیمه هستند.

اصول محاسبه حق‌بیمه

اگر متغیر تصادفی x بیانگر مقدار خسارت با تابع توزیع F(x) باشد و E(x) و Var(x) به ترتیب میانگین و واریانس توزیع باشند آنگاه اصول محاسبه حق‌بیمه به شرح زیر هستند:

1. ساده ترین روش محاسبه حق‌بیمه، حق‌بیمه خالص است و برابر خسارت مورد انتظار می باشد یعنی:

P= E(x)

مقدار خسارت مورد انتظار در بیمه‌های زندگی و بعضی از بیمه های غیر زندگی کاربرد دارد. اما با توجه به نظریه ورشکستگی شرکت‌های بیمه ( (ruin theory، حق‌بیمه خالص بدون در نظرگرفتن هزینه‌ها و عوامل سربار (loading) ناکافی خواهد بود چرا که در درازمدت وقوع ورشکستگی حتی در صورت داشتن ذخایر حتمی خواهد بود.

2. از آنجا که ممکن است مقدار خسارت واقعی با مقدار مورد انتظار بیمه گر متفاوت باشد، بیمه‌گر باید به خاطر این عدم اطمینان مقدار سرباری را برای حق‌بیمه در نظر بگیرد. بنابرای به منظور در نظر گرفتن این مسئله فرمول حق‌بیمه خالص به اضافه سربار عدم اطمینان به صورت زیر خواهد بود که یک تابع صعودی از a است:

P= (1+a)E(X)

به این مقدار، حق‌بیمه با سربار ایمنی (premium with safety loading) گفته می‌شود.